Dr. Bogdan Teaca

Applied Mathematics & Theoretical Physics

Understanding Interactions in Turbulence

Understanding the motion of electrically charged particles in a plasma medium is crucial for the study of solar and astrophysical phenomena (e.g. the solar wind, sun corona heating, cosmic rays transport), but also for the development of controlled fusion energy, one of the largest and most important engineering endeavors of this century.

As electrically charged particles move, they generate electromagnetic fields that in turn affect the trajectories of the charged particles. Thus, plasmas represent the cumulative interplay occurring between charged particles and electromagnetic fields. The description of a plasma can range from the simpler fluid approaches (magnetohydrodynamics) to complex gyrokinetic formalisms, where phase space dynamics and symmetries become important.

At the core of the problem stands the impact made on the particles by the intricate electromagnetic structures, generated self-consistently by the turbulent motion of a plasma flow. Even for air or water, the nonlinear nature of turbulence leads to a self-organization of energetic structures, best seen as vortices or eddies. In plasmas, turbulence exhibits an even more complex nature, as it also manifests itself at the level of the electromagnetic fields.

To understand turbulence we need to understand the interactions that occur between different scales in a system. For this we use different diagnostics that measure the energy redistribution between scales and its eventual anisotropic behavior, the degree of scale locality for interactions and the phase space structure for kinetic systems.

To tackle the problem, we use numerical simulations of complex nonlinear dynamical systems. Computationally, a wide range of resources is used, from small workstations to massive supercomputers (parallelized simulations can use on the order of one thousand processors for one run). Thus, code development represents an important part of our work.

At present, our research is centered on understanding the self-organization nature of plasmas, the fundamental nature of interactions between different scales in kinetic turbulence and the impact these have on fusion and astrophysical problems of interest.

Astrophysical Plasma Heating

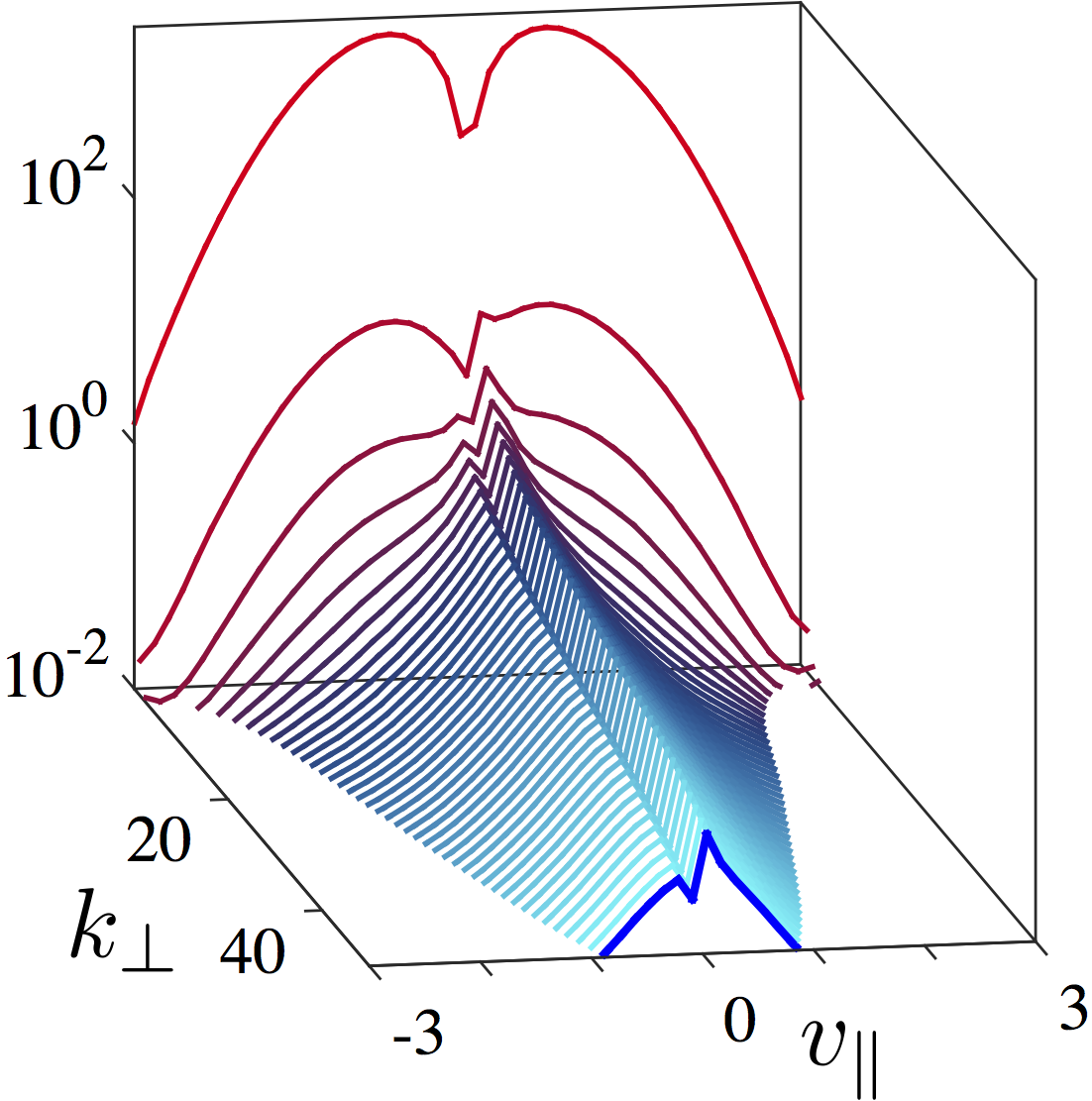
The radial temperature profile of the solar wind, as measured by spacecraft, can only be explained by the presence of heating throughout the heliosphere. Identifying the physical mechanisms that dissipate small-scale turbulent fluctuations, ultimately converting the turbulent energy into heat, is thus one of the major unsolved problems in the solar wind community. Because of the low collisionality of the solar wind, a kinetic model is necessary to understand the effects that contribute to the heating of the plasma. Over the past years, a major effort has been put into computational studies of the problem using fully kinetic and gyrokinetic systems.

Using gyrokinetic simulations, we obtained evidence that the locations of current sheets (defined as regions of high current) do not generally correspond to peaks in the electron and ion heating rates.

Furthermore, we show that plasma heating is highly anisotropic in velocity space, providing first time direct measurements that identify the dominant collisional direction for each species. We identified Landau damping as the preferred route for the electron heating, while nonlinear (perpendicular) phase mixing is the channel responsible for ion heating. These results demonstrate the importance of kinetic dynamics.

This is a work done together with Alejandro Bañón Navarro (Max Planck Institute for Plasma Physics), Daniel Told (Max Planck Institute for Plasma Physics), Daniel Groselj (Max Planck Institute for Plasma Physics), Frank Jenko (Max Planck Institute for Plasma Physics).

Particle Acceleration in Turbulence

Turbulence in plasma exhibits structures in the electromagnetic fields that affect the transport and acceleration of particles. This is a problem of particular interest in astrophysics, where the scattering of cosmic rays affect our ability to make correct observations.

While the force that acts on a charged particle is simple, i.e. the Lorentz force, the intricacy of turbulence makes the problem far from trivial. One of the effect of interest is that of ideal invariants in turbulence, i.e. qualities that are preserved in the absence of viscosity and field line diffusivity, and how their levels affect the properties of structures observed. Cross helicity was shown to affect the acceleration rate of particles and magnetic helicity is expected to have a similar effect.

This is a work done together with Martin S. Weidl (Max Planck Institute for Plasma Physics), Frank Jenko (Max Planck Institute for Plasma Physics) and Reinhard Schlickeiser (Ruhr University Bochum).

Modeling Turbulence in Tokamaks

Turbulence is characterized by the nonlinear coupling of scales over a large interval. While geometric effects matter at large scales, small scales tend to recover more universal characteristics to them. This universality allows us to model small scales of turbulence and their energetic coupling with the larger scales, which are solved numerically. This idea is at the cornerstone of Large Eddy Simulations (LES).

Since tokamaks are complex machines from a geometrical perspective and are described by five-dimensional kinetic theories, LES methods offer more affordable ways to perform routine numerical simulations.

This is a work done together with Alejandro Bañón Navarro (Max Planck Institute for Plasma Physics), Frank Jenko (Max Planck Institute for Plasma Physics) and Gregory W. Hammett (Princeton University).

Subcritical Plasma Flows

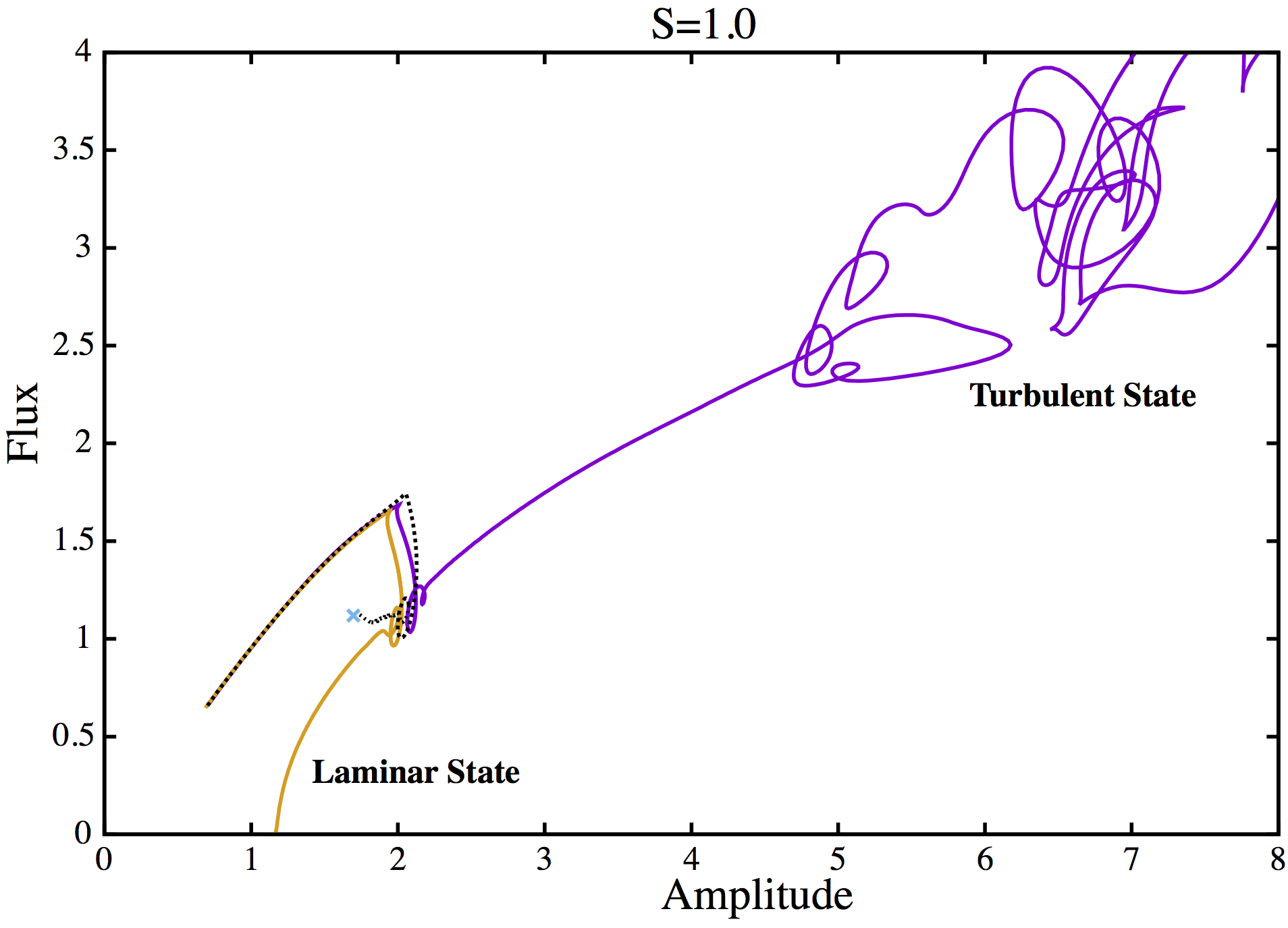
Sheared flows perpendicular to the driving temperature gradients can strongly stabilise the linear physics in plasma. While the system is linearly stable, regimes with persistent nonlinear turbulence may develop, i.e. the system is subcritical.

A perturbation with small but finite amplitude may be sufficient to push the plasma into a regime where nonlinear effects are dominant and thus allow sustained turbulence.

At the critical amplitude, instead of transitioning to the turbulent regime or decaying to a laminar state, the trajectory will map out the edge of chaos and the solution will stay on the edge (x mark on figure).

Depending on the parameter of the system (the shear S for example) the flow in subcritical plasma can exhibit simple localized advecting structures or fill the entire volume. The transition between the two states is important from practical and theoretical considerations.

This is a work done together with Chris C. Pringle (Coventry University) and Ben McMillan (University of Warwick).